Category: Bank Capital

Bank funding costs and capital structure – what I missed

A recent post looked at a Bank of England paper that offered evidence that the cost of higher capital requirements will be mitigated by a reduction in leverage risk which translates into lower borrowing costs and a decline in the required return equity. My post set out some reasons why I struggled with this finding.

My argument was that,

  • in banking systems where the senior debt rating of banks assumed to be Too Big To Fail is supported by an implied assumption of government support (such as Australia),
  • increasing the level of subordinated debt could reduce the value of that implied support,
  • however, senior debt itself does not seem to be any less risky (the senior debt rating does not improve), and
  • the subordinated debt should in theory be more risky if it reduces the value of the assumption of government support.

Fortunately, I also qualified my observations with the caveat that it was possible that I was missing something. Recent issuance of Tier 2 debt by some Australian banks offers some more empirical evidence that does seem to suggest that the cost of senior debt can decline in response to the issuance of more junior securities and that the cost of subordinated debt does not seem to be responding in the way that the theory suggests.

My original argument was I think partly correct. The prospect of the large Australian banks substantially increasing the relative share of Tier 2 debt in their liability structure has not resulted in any improvement in the AA- senior debt rating of the banks subject to this Total Loss Absorbing Capital requirement. So senior debt does not seem to be any less risky.

What I missed was the impact of the supply demand dynamic in a low interest rate environment where safe assets are in very short supply.

The senior debt in my thesis is no less risky but the debt market appears to be factoring in the fact that the pool of AA- senior debt is likely to shrink relative to what was previously expected. Investors who have been struggling for some time to find relatively safe assets with a decent yield weigh up the options. A decent yield on safe assets like they used to get in the old days would obviously be preferable but that is not on offer so they pay up to get a share of what is on offer.

The subordinated debt issued by these banks might be more risky in theory to the extent that bail-in is now more credible but if you do the analysis and conclude that the bank is well managed and low risk then you discount the risk of being bailed-in and take the yield. Again the ultra low yield on very safe assets and the shortage of better options means that you probably bid strongly to get a share of the yield on offer.

Summing up. The impacts on borrowing costs described here may look the same as what would be expected if the Modigliani-Miller effect was in play but the underlying driver appears to be something else.

It remains possible that I am still missing something but hopefully this post moves me a bit closer to a correct understanding of how capital structure impacts bank funding costs …

Tony

Is the financial system as resilient as policymakers say?

This is the question that Sir Paul Tucker poses in a BIS Working Paper titled “Is the financial system sufficiently resilient: a research programme and policy agenda” (BIS WP790) and answers in the negative. Tucker’s current role as Chair of the Systemic Risk Council and his experience as Deputy Governor at the Bank of England from 2009 to 2013 suggests that, whether you agree or disagree, it is worth reading what he has to say.

Tucker is quick to acknowledge that his assessment is “… intended to jolt the reader” and recognises that he risks “… overstating weaknesses given the huge improvements in the regulatory regime since 2007/08”. The paper sets out why Tucker believes the financial system is not as resilient as claimed, together with his proposed research and policy agenda for achieving a financial system that is sufficiently resilient.

Some of what he writes is familiar ground but three themes I found especially interesting were:

  1. The extent to which recourse by monetary policy to very low interest rates exposes the financial system to a cyclically higher level of systemic risk that should be factored into the resilience target;
  2. The need to formulate what Tucker refers to as a “Money Credit Constitution” ; and
  3. The idea of using “information insensitivity” for certain agreed “safe assets” as the target state of resilience for the system.

Financial stability is of course one of those topics that only true die hard bank capital tragics delve into. The Global Financial Crisis (GFC) demonstrated, however, that financial stability and the resilience of the banking system is also one of those topics that impacts every day life if the technocrats get it wrong. I have made some more detailed notes on the paper here for the technically inclined while this post will attempt (and likely fail) to make the issues raised accessible for those who don’t want to read BIS working papers.

Of the three themes listed above, “information insensitivity” is the one that I would call out in particular. It is admittedly a bit clunky as a catch phrase but I do believe it is worth investing the time to understand what it means and what it implies for how the financial system should be regulated and supervised. I have touched on the concept in a couple of previous posts (here, here, and here) and, as I worked through this post, I also found some interesting overlaps with the idea introduced by the Australian Financial System Inquiry that systemically important banks should be required to be “unquestionably strong”.

How resilient is the financial system?

Tucker’s assessment is that Basel III has made the financial system a lot safer than it was but less resilient than claimed. This is because the original calibration of the higher capital requirements under Basel III did not allow for the way in which any subsequent reduction in interest rates means that monetary policy has less scope to help mitigate economic downturns. All other things being equal, any future stress will have a larger impact on the financial system because monetary policy will have less capacity to stimulate the economy.

We could quibble over details:

  • The extent to which the capital requirements have been increased by higher Risk Weights applied to exposures (Tucker is more concerned with the extent to which capital requirements get weakened over time in response to industry lobbying)
  • Why is this not captured in stress testing?
  • The way in which cyclical buffers could (and arguably should) be used to offset this inherent cyclical risk in the financial system.

But his bigger point sounds intuitively right, all other things being equal, low interest rates mean that central banks will have much less scope to stimulate the economy via monetary policy. It follows that the financial system is systemically riskier at this point in time than historical experience with economic downturns might suggest.

How should we respond (in principle)?

One response is common equity and lots of it. That is what is advocated by some academic commentators , influential former central bankers such as Adair Turner and Mervyn King, and most recently by the RBNZ (with respect to the quantum and the form of capital.

Tucker argues that the increased equity requirements agreed under Basel III are necessary, but not sufficient. His point here is broader than the need to allow for changes in monetary policy discussed above. His concern is what does it take to achieve the desired level of resilience in a financial system that has fractional reserve banking at its core.

”Maintaining a resilient system cannot sanely rely on crushing the probability of distress via prophylactic regulation and supervision: a strategy that confronts the Gods in its technocratic arrogance. Instead, low barriers to entry, credible resolution regimes and crisis-management tools must combine to ensure that the system can keep going through distress. That is different from arguing that equity requirements (E) can be relaxed if resolution plans become sufficiently credible. Rather, it amounts to saying that E would need to be much higher than now if resolution is not credible.”

“Is the Financial system sufficiently resilient: a research programme and policy agenda” BIS WP 790, p 23

That is Tucker’s personal view expressed in the conclusion to the paper but he also advocates that “unelected technicians need to frame the question [of target resilience] in a digestible way for politicians and public debate“. It is especially important that the non-technical people understand the extent to which there may be trade-offs in the choice of how resilient the financial system should be. Is there, for example, a trade-off between resilience and the dynamism of the financial system that drives its capacity to support innovation, competition and growth? Do the resource misallocations associated with credit and property price booms damage the long run growth of the economy? And so on …

Turner offers a first pass at how this problem might be presented to a non-technical audience:

Staying with crisp oversimplification, I think the problem can be put as follows:

• Economists and policymakers do not know much about this. Models and empirics are needed.

• Plausibly, as BIS research suggests, credit and property price booms lead resource misallocation booms? Does that damage long-run growth?

• Even if it does, might those effects be offset by net benefits from greater entrepreneurship during booms?

• Would tough resilience policies constrain capital markets in ways that impede the allocation of resources to risky projects and so growth?

If there is a long-run trade off, then where people are averse to boom-bust ‘cycles’, resilience will be higher and growth lower. By contrast, jurisdictions that care more about growth and dynamism will err on the side of setting the resilience standard too low.

BIS WP790, Page 5

He acknowledges there are no easy answers but asking the right questions is obviously a good place to start.

A “Money-Credit Constitution”

In addition to helping frame the broader parameters of the problem for public debate, central bankers also need to decide what their roles and responsibilities in the financial system should be. Enter the idea of a Money-Credit Constitution (MCC). I have to confess that this was a new bit of jargon for me and I had to do a bit of research to be sure that I knew what Tucker means by it. The concept digs down into the technical aspects of central banking but it also highlights the extent to which unelected technocrats have been delegated a great deal of power by the electorate. I interpret Tucker’s use of the term “constitution”as an allusion to the need for the terms on which this power is exercised to be defined and more broadly understood.

A Money-Credit Constitution defined:

“By that I mean rules of the game for both banking and central banking designed to ensure broad monetary stability, understood as having two components: stability in the value of central bank money in terms of goods and services, and also stability of private-banking-system deposit money in terms of central bank money.”

Chapter 1: How can central banks deliver credible commitment and be “Emergency Institutions”? by John Tucker in “Central Bank Governance and Oversight Reform, edited by Cochrane and Taylor (2016)

The jargon initially obscured the idea (for me at least) but some practical examples helped clarify what he was getting at. Tucker defines the 19th and early 20th century MCC as comprising; the Gold Standard, reserve requirements for private banks and the Lender of Last Resort (LOLR) function provided by the central bank. The rules of the game (or MCC) have of course evolved over time. In the two to three decades preceding the 2008 GFC, the rules of the game incorporated central bank independence, inflation targeting and a belief in market efficiency/discipline. Key elements of that consensus were found to be woefully inadequate and we are in the process of building a new set of rules.

Tucker proposes that a MCC that is fit for the purpose of achieving an efficient and resilient financial system should have five key components:

– a target for inflation (or some other nominal magnitude);

– a requirement for banking intermediaries to hold reserves (or assets readily exchanged for reserves) that increases with a firm’s leverage and/or the degree of liquidity mismatch between its assets and liabilities;

– a liquidity-reinsurance regime for fundamentally solvent banking intermediaries;

– a resolution regime for bankrupt banks and other financial firms; and

– constraints on how far the central bank is free to pursue its mandate and structure its balance sheet, given that a monetary authority by definition has latent fiscal capabilities.

BIS WP, Page 9

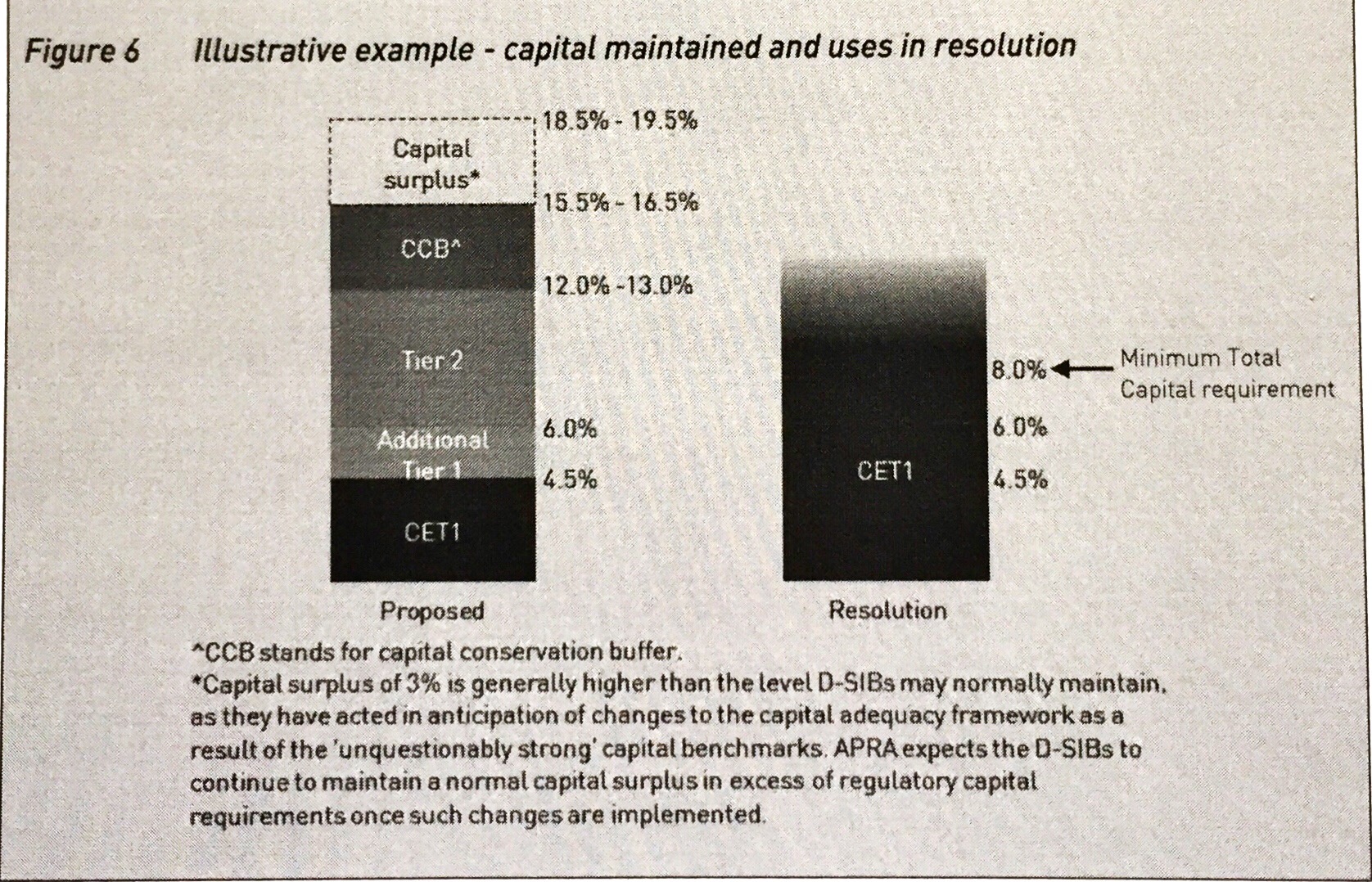
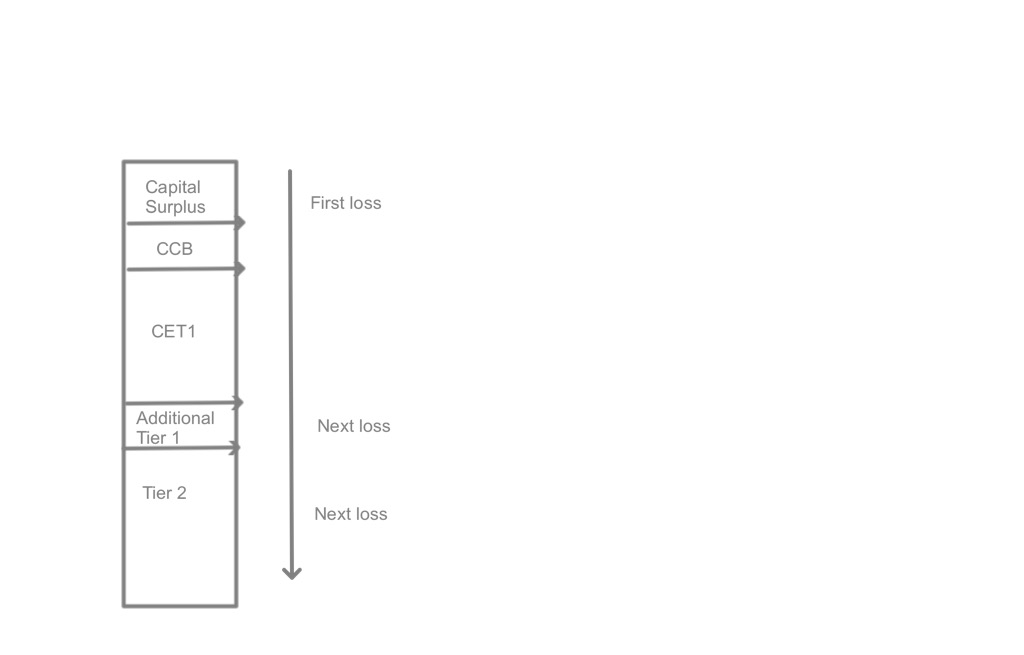
In one sense, the chosen resilience strategy for the financial system is simply determined by the combination of the capital and liquidity requirements imposed on private banks. We are using the term capital here in its broadest sense to incorporate not just common equity but also the various forms of hybrid equity and subordinated debt that can be converted into equity without disrupting the financial system.

But Tucker argues that there is a bigger question of strategy that must be addressed; that is

“whether to place the regime’s weight on regulatory requirements that impose intrinsic resilience on bank balance sheets or on credible crisis management that delivers safety ex post. It is a choice with very different implications for transparency.”

BIS WP 790; Page 11

Two alternative strategies for achieving a target state of financial system resilience

Strategy 1: Crisis prevention (or mitigation at least)

The first strategy is essentially an extension of what we have already been doing for some time; a combination of capital and liquidity requirements that limits the risk of financial crisis to some pre-determined acceptable level.

“… authorities set a regulatory minimum they think will be adequate in most circumstances and supervise intermediaries to check whether they are exposed to outsized risks.

BIS WP 790, Page 11

Capital and liquidity requirements were increased under Basel III but there was nothing fundamentally new in this part of the Basel III package. Tucker argues that the standard of resilience adopted should be explicit rather than implicit but he still doubts that this strategy is robust. His primary concern seems to be the risk that the standard of resilience is gradually diluted by a series of small concessions that only the technocrats understand.

“How did we know that firms are really satisfying the standard: is it enough that they say so? And how do we know that the authorities themselves have not quietly diluted or abandoned the standard?”

BIS WP 790; Page 11

Tucker has ideas for how this risk of regulatory capture might be controlled:

  each year central bank staff (not policymakers) should publish a complete statement of all relaxations and tightenings of regulatory and supervisory policy (including in stress testing models, rules, idiosyncratic requirements, and so on)

  the integrity of such assessments should be subject to external audit of some kind (possibly by the central auditor for the state).

BIS WP 790, Page 12

… but this is still a second best approach in his assessment; he argues that we can do better and the idea of making certain assets “informationally insensitive” is the organising principle driving the alternative strategies he lays out.

Strategy 2: Making assets informationally insensitive via crisis-management regimes

Tucker identifies two approaches to crisis management both based around the objective of ensuring that the value of certain agreed liabilities, issued by a defined and pre-determined set of financial intermediaries, is insensitive to information about the financial condition of these intermediaries:

Strategy 2a: Integrate LOLR with liquidity policy.

Central bankers, as the suppliers of emergency liquidity assistance, could make short term liabilities informationally insensitive by requiring banks to hold reserves or eligible collateral against all runnable liabilities. Banks would be required to cover “x”% of short term liabilities with reserves and/or eligible collateral. The key policy choices then become

  • The definition of which short term liabilities drive the liquidity requirement;
  • The instruments that would be eligible collateral for liquidity assistance; and
  • The level of haircuts set by central banks against eligible collateral

What Tucker is outlining here is a variation on a proposal that Mervyn King set out in his book “The End of Alchemy” which I covered in a previous post. These haircuts operate broadly analogously to the existing risk-weighted equity requirements. Given the focus on emergency requirements, they would be based on stress testing and incorporate systemic risk surcharges.

Tucker is not however completely convinced by this approach:

“… a policy of completely covering short-term labilities with central bank-eligible assets would leave uninsured short-term liabilities safe only when a bank was sound. They would not be safe when a bank was fundamentally unsound.

That is because central banks should not (and in many jurisdictions cannot legally) lend to banks that have negative net assets (since LOLR assistance would allow some short-term creditors to escape whole at the expense of equally ranked longer-term creditors). This is the MCC’s financial-stability counterpart to the “no monetary financing” precept for price stability.

Since only insured-deposit liabilities, not covered but uninsured liabilities, are then safe ex post, uninsured liability holders have incentives to run before the shutters come down, making their claims information sensitive after all.

More generally, the lower E, the more frequently banks will fail when the central bank is, perforce, on the sidelines. This would appear to take us back, then, to the regulation and supervision of capital adequacy, but in a way that helps to keep our minds on delivering safety ex post and so information insensitivity ex ante.”

BIS WP 790, Page 14

Strategy 2b: Resolution policy – Making operational liabilities informationally insensitive via structure

Tucker argues that the objective of resolution policy can be interpreted as making the operational liabilities of banks, dealers and other intermediaries “informationally insensitive”. He defines “operational liabilities” as “… those liabilities that are intrinsically bound to the provision of a service (eg large deposit balances, derivative transactions) or the receipt of a service (eg trade creditors) rather than liabilities that reflect a purely risk-based financial investment by the creditor and a source of funding/leverage for the bank or dealer”

Tucker proposes that this separation of operational liabilities from purely financial liabilities can be “… made feasible through a combination of bail-in powers for the authorities and, crucially, restructuring large and complex financial groups to have pure holding companies that issue the bonds to be bailed-in” (emphasis added).

Tucker sets out his argument for structural subordination as follows.

“…provided that the ailing operating companies (opcos) can be recapitalised through a conversion of debt issued to holdco …., the opcos never default and so do not go into a bankruptcy or resolution process. While there might be run once the cause of the distress is revealed, the central bank can lend to the recapitalised opco …

This turns on creditors and counterparties of opcos caring only about the sufficiency of the bonds issued to the holdco; they do not especially care about any subsequent resolution of the holding company. That is not achieved, however, where the bonds to be bailed in … are not structurally subordinated. In that respect, some major jurisdictions seem to have fallen short:

  Many European countries have opted not to adopt structural subordination, but instead have gone for statutory subordination (eg Germany) or contractual subordination (eg France).

  In consequence, a failing opco will go into resolution

  This entails uncertainty for opco liability holders given the risk of legal challenge etc

  Therefore, opco liabilities under those regimes will not be as informationally insensitive as would have been possible.

BIS WP 790, Page 15

While structural subordination is Tucker’s preferred approach, his main point is that the solution adopted should render operational liabilities informationally insensitive:

“….the choice between structural, statutory and contractual subordination should be seen not narrowly in terms of simply being able to write down and/or convert deeply subordinated debt into equity, but rather more broadly in terms of rendering the liabilities of operating intermediaries informationally insensitive. The information that investors and creditors need is not the minutiae of the banking business but the corporate finance structure that enables resolution without opcos formally defaulting or going into a resolution process themselves

BIS WP 790 , Pages 15-16

If jurisdictions choose to stick with contractual or statutory subordination, Tucker proposes that they need to pay close attention to the creditor hierarchy, especially where the resolution process is constrained by the requirement that no creditor should be worse off than would have been the case in bankruptcy. Any areas of ambiguity should be clarified ex ante and, if necessary, the granularity of the creditor hierarchy expanded to ensure that the treatment of creditors in resolution is what is fair, expected and intended.

Tucker sums up the policy implications of this part of his paper as follows ...

“The policy conclusion of this part of the discussion, then, is that in order to deliver information insensitivity for some of the liabilities of operating banks and dealers, policymakers should:

a) move towards requiring that all short-term liabilities be covered by assets eligible at the central bank; and, given that that alone cannot banish bankruptcy,

b) be more prescriptive about corporate structures and creditor hierarchies since they matter hugely in bankruptcy and resolution.”

BIS WP 790, Page 16

Summing up …

  • Tucker positions his paper as “… a plea to policymakers to work with researchers to re-examine whether enough has been done to make the financial system resilient“.
  • His position is that “… the financial system is much more resilient than before the crisis but … less resilient than claimed by policymakers”
  • Tucker’s assessment “… is partly due to shifts in the macroeconomic environment” which reduce the capacity of monetary and fiscal policy stimulus but also an in principle view that “maintaining a resilient system cannot sanely rely on crushing the probability of distress via prophylactic regulation and supervision: a strategy that confronts the Gods in its technocratic arrogance“.
  • Tucker argues that the desired degree of resilience is more likely to be found in a combination of “… low barriers to entry, credible resolution regimes and crisis management tools …[that] … ensure the system can keep going through distress”.
  • Tucker also advocates putting the central insights of some theoretical work on “informational insensitivity” to practical use in the following way:
    • move towards requiring all banking-type intermediaries to cover all short-term liabilities with assets eligible for discount at the Window
    • insist upon structural subordination of bailinable bonds so that the liabilities of operating subsidiaries are more nearly informationally insensitive
    • be more prescriptive about the permitted creditor hierarchy of operating intermediaries
    • establish frameworks for overseeing and regulating collateralised money market, with more active use made of setting minimum haircut requirements to ensure that widely used money market instruments are safe in nearly all circumstancesarticulating restrictive principles for market-maker of last resort operations
  • Given the massive costs (economic, social, cultural) associated with financial crises, err on the side of maintaining resilience
  • To the extent that financial resilience continues to rely on the regulation and supervision of capital adequacy, ensure transparency regarding the target level of resilience and the extent to which discretionary policy actions impact that level of resilience

I am deeply touched if you actually read this far. The topic of crisis management and resolution capability is irredeemably technical but also important to get right.

Tony

Automatic stabilisers in banking capital | VOX, CEPR Policy Portal

I am in favour of cyclical capital buffers but not the kind the BCBS has developed.

I have attached a link to a post by Charles Goodhart and Dirk Schoenmaker which highlights the problems with the BCBS Counter Cyclical Capital Buffer (CCyB) and proposes an alternative more rules based approach.

While banking is procyclical, the capital framework is largely static. The countercyclical capital buffer is discretionary, with potential danger of inaction, and is also limited in scale. This column proposes an expanded capital conservation buffer, which would act as an automatic stabiliser. This could incorporated in the next Basel review and the upcoming Solvency II review.

I have my own preferred alternative approach to the cyclical buffer problem but I agree very much with their critique of the CCyB.

Their post on this question is not long but worth reading.

— Read on voxeu.org/article/automatic-stabilisers-banking-capital

Tony

Mortgage risk weight fact check – APRA’s perspective

I have posted a number of times on the extent to which the differential between mortgage risk weights applied to large and small banks is as big as is (repeatedly) asserted. APRA’s response to submissions on “Revisions to the capital framework for authorised deposit-taking institutions” (released 9 June 2019) has what I hope will be the definitive statement on the extent and justification for this difference.

I have copied the entire APRA comment on this differential below but the short version is that APRA does not see the difference being as large as it is claimed to be.

“When looked at holistically, the existing differential between the standardised and IRB approaches is small. While the precise calibration of the risk weights remains subject to further analysis, it is APRA’s intention that any differential in overall capital requirements, and hence any impact on pricing by standardised and IRB ADIs, will remain negligible.”

So far, it seems that the argument I have been making for some time on this question stands. Read on if you want more detail.

Risk weight differential in mortgage lending

For some time, there has been considerable interest in the impact, from a competition perspective, of the differential between standardised and IRB risk weights for mortgage lending.

Commentary on this issue has often focussed on the differential in average risk weights between ADIs using the two approaches. Superficially, this suggests a material differential exists. However, by only examining risk weights for on-balance sheet exposures, the impact of other important differences is ignored.

Beyond prescribed risk weights, differences in capital requirements for mortgage lending are driven by:

• differences in the credit quality of the underlying portfolio;

• differences in the ‘unquestionably strong’ capital benchmarks applied to standardised and IRB ADIs;

• differences in the treatment of credit conversion factors (CCFs) for standardised and IRB ADIs;

• the application of capital requirements for IRRBB to IRB, but not standardised, ADIs; and

• the requirement for an expected loss adjustment for IRB, but not standardised, ADIs.

Ignoring any differences in portfolio quality, each of the above factors serves to narrow any impact from standardised risk weights being higher than IRB risk weights. Under the current regulatory framework (i.e. before applying the proposals in this paper), APRA estimates that the impact of the overall difference in capital requirements on mortgage pricing is likely to be minimal – in the order of 5 basis points.

The analysis does not consider the operational costs arising from investing in developing and maintaining risk management systems to support IRB status, as well as data requirements.

Furthermore, the application of an additional capital buffer to those banks designated a domestically systemically important further narrows, if not completely eliminates, the overall difference for those banks.

APRA does not expect the changes proposed in this paper to materially change the above conclusions. When looked at holistically, the existing differential between the standardised and IRB approaches is small. While the precise calibration of the risk weights remains subject to further analysis, it is APRA’s intention that any differential in overall capital requirements, and hence any impact on pricing by standardised and IRB ADIs, will remain negligible.

Mortgage risk weights fact check revisited – again

The somewhat arcane topic of mortgage risk weights is back in the news. It gets popular attention to the extent they impact the ability of small banks subject to standardised risk weights to compete with bigger banks which are endorsed to use the more risk sensitive version based on the Internal Ratings Based (IRB) approach. APRA released a Discussion Paper (DP) in February 2018 titled “Revisions to the capital framework for authorised deposit-taking institutions”. There are reports that APRA is close to finalising these revisions and that this will address the competitive disadvantage that small banks suffer under the current regulation.

This sounds like a pretty simple good news story – a victory for borrowers and the smaller banks – and my response to the discussion paper when it was released was that there was a lot to like in what APRA proposed to do. I suspect however that it is a bit more complicated than the story you read in the press.

The difference in capital requirements is overstated

Let’s start with the claimed extent of the competitive disadvantage under current rules. The ACCC’s Final Report on its “Residential Mortgage Price Inquiry” described the challenge with APRA’s current regulatory capital requirements as follows:

“For otherwise identical ADIs, the advantage of a 25% average risk weight (APRA’s minimum for IRB banks) compared to the 39% average risk weight of standardised ADIs is a reduction of approximately 0.14 percentage points in the cost of funding the loan portfolio. This difference translates into an annual funding cost advantage of almost $750 on a residential mortgage of $500 000, or about $15 000 over the 30 year life of a residential mortgage (assuming an average interest rate of 7% over that period).”

You could be forgiven for concluding that this differential (small banks apparently required to hold 56% more capital for the same risk) is outrageous and unfair.

Just comparing risk weights is less than half the story

I am very much in favour of a level playing field and, as stated above, I am mostly in favour of the changes to mortgage risk weights APRA outlined in its discussion paper but I also like fact based debates.

While the risk weights for big banks are certainly lower on average than those required of small banks, the difference in capital requirements is not as large as the comparison of risk weights suggests. To understand why the simple comparison of risk weights is misleading, it will be helpful to start with a quick primer on bank capital requirements.

The topic can be hugely complex but, reduced to its essence, there are three elements that drive the amount of capital a bank holds:

  1. The risk weights applied to its assets
  2. The target capital ratio applied to those risk weighted assets
  3. Any capital deductions required when calculating the capital ratio

I have looked at this question a couple of times (most recently here) and identified a number of problems with the story that the higher risk weights applied to residential mortgages originated by small bank places them at a severe competitive disadvantage:

Target capital ratios – The target capital adequacy ratios applied to their higher standardised risk weighted assets are in some cases lower than the IRB banks and higher in others (i.e. risk weights alone do not determine how much capital a bank is required to hold).

Portfolio risk – The risk of a mortgage depends on the portfolio not the individual loan. The statement that a loan is the same risk irrespective of whether it is written by a big bank or small bank sounds intuitively logical but is not correct. The risk of a loan can only be understood when it is considered as part of the portfolio the bank holds. All other things being equal, small banks will typically be less diversified and hence riskier than a big bank.

Capital deductions – You also have to include capital deductions and the big banks are required to hold capital for a capital deduction linked to the difference between their loan loss provisions and a regulatory capital value called “Regulatory Expected Loss”. The exact amount varies from bank to bank but I believe it increases the effective capital requirement by 10-12% (i.e. an effective RW closer to 28% for the IRB banks).

IRRBB capital requirement – IRB banks must hold capital for Interest Rate Risk in the Banking Book (IRRBB) while the small standardised banks do not face an explicit requirement for this risk. I don’t have sufficient data to assess how significant this is, but intuitively I would expect that the capital that the major banks are required to hold for IRRBB will further narrow the effective difference between the risk weights applied to residential mortgages.

How much does reducing the risk weight differential impact competition in the residential mortgage market?

None of the above is meant to suggest that the small banks operating under the standardised approach don’t have a case for getting a lower risk weight for their higher quality lower risk loans. If the news reports are right then it seems that this is being addressed and that the gap will be narrower. However, it is important to remember that:

  • The capital requirement that the IRB banks are required to maintain is materially higher than a simplistic application of the 25% average risk weight (i.e. the IRB bank advantage is not as large as it is claimed to be).
  • The standardised risk weight does not seem to be the binding constraint so reducing it may not help the small banks much if the market looks through the change in regulatory risk measurement and concludes that nothing has changed in substance.

One way to change the portfolio quality status quo is for small banks to increase their share of low LVR loans with a 20% RW. Residential mortgages do not, for the most part, get originated at LVR of sub 50% but there is an opportunity for small banks to try to refinance seasoned loans where the dynamic LVR has declined. This brings us to the argument that IRB banks are taking the “cream” of the high quality low risk lending opportunities.

The “cream skimming” argument

A report commissioned by COBA argued that:

“While average risk weights for the major banks initially rose following the imposition of average risk weight on IRB banks by APRA, two of the major banks have since dramatically reduced their risk weights on residential mortgages with the lowest risk of default. The average risk weights on such loans is now currently on average less than 6 per cent across the major banks.”

“Despite the imposition of an average risk weight on residential home loans, it appears some of the major banks have decided to engage in cream skimming by targeting home loans with the lowest risk of default. Cream skimming occurs when the competitive pressure focuses on the high-demand customers (the cream) and not on low- demand ones (the skimmed milk) (Laffont & Tirole, 1990, p. 1042). Cream skimming has adverse consequences as it skews the level of risk in house lending away from the major banks and towards other ADIs who have to deal with an adversely selected and far riskier group of home loan applicants.”

“Reconciling Prudential Regulation with Competition” prepared by Pegasus Economics May 2019 (page 43)

It is entirely possible that I am missing something here but, from a pure capital requirement perspective, it is not clear that IRB banks have a material advantage in writing these low risk loans relative to the small bank competition. The overall IRB portfolio must still meet the 25% risk weight floor so any loans with 6% risk weights must be offset by risk weights (and hence riskier loans) that are materially higher than the 25% average requirement. I suspect that the focus on higher quality low risk borrowers by the IRB banks was more a response to the constraints on capacity to lend than something that was driven by the low risk weights themselves.

Under the proposed revised requirements, small banks in fact will probably have the advantage in writing sub 50% LVR loans given that they can do this at a 20% risk weight without the 25% floor on their average risk weights and without the additional capital requirements the IRB banks face.

I recognise there are not many loans originated at this LVR band but there is an opportunity in refinancing seasoned loans where the combined impact of principal reduction and increased property value reduces the LVR. In practice the capacity of small banks to do this profitably will be constrained by their relative expense and funding cost disadvantage. That looks to me to be a bigger issue impacting the ability of small banks to compete but that lies outside the domain of regulatory capital requirements.

Maybe this potential arbitrage does not matter in practice but APRA could quite reasonably impose a similar minimum average RW on Standardised Banks if the level playing field argument works both ways. This should be at least 25% but arguably higher once you factor in the fact that the small banks do not face the other capital requirements that IRB banks do. Even if APRA did not do this, I would expect the market to start looking more closely at the target CET1 for any small bank that accumulated a material share of these lower risk weight loans.

Implications

Nothing in this post is meant to suggest that increasing the risk sensitivity of the standardised risk weights is a bad idea. It seems doubtful however that this change alone will see small banks aggressively under cutting large bank competition. It is possible that small bank shareholders may benefit from improved returns on equity but even that depends on the extent to which the wholesale markets do not simply look through the change and require smaller banks to maintain the status quo capital commitment to residential mortgage lending.

What am I missing …

Every bank needs a cyclical capital buffer

This post sets out a case for a bank choosing to incorporate a discretionary Cyclical Buffer (CyB) into its Internal Capital Adequacy Assessment Process (ICAAP). The size of the buffer is a risk appetite choice each individual bank must make. The example I have used to illustrate the idea is calibrated to absorb the expected impact of an economic downturn that is severe but not necessarily a financial crisis style event. My objective is to illustrate the ways in which incorporating a Cyclical Buffer in the target capital structure offers:

  • an intuitive connection between a bank’s aggregate risk appetite and its target capital structure;
  • a means of more clearly defining the point where losses transition from expected to unexpected; and
  • a mechanism that reduces both the pro cyclicality of a risk sensitive capital regime and the tendency for the transition to unexpected losses to trigger a loss of confidence in the bank.

The value of improved clarity, coherence and consistency in the risk appetite settings is I think reasonably self evident. The need for greater clarity in the distinction between expected and unexpected loss perhaps less so. The value of this Cyclical Buffer proposal ultimately depends on its capacity to enhance the resilience of the capital adequacy regime in the face of economic downturns without compromising its risk sensitivity.

There are no absolutes when we deal with what happens under stress but I believe a Cyclical Buffer such as is outlined in this post also has the potential to help mitigate the risk of loss of confidence in the bank when losses are no longer part of what stakeholders expect but have moved into the domain of uncertainty. I am not suggesting that this would solve the problem of financial crisis. I am suggesting that it is a relatively simple enhancement to a bank’s ICAAP that has the potential to make banks more resilient (and transparent) with no obvious downsides.

Capital 101

In Capital 101, we learn that capital is meant to cover “unexpected loss” and that there is a neat division between expected and unexpected loss. The extract below from an early BCBS publication sets out the standard explanation …

Expected and unexpected credit loss

Figure 1 – Expected and Unexpected Loss

The BCBS publication from which this image is sourced explained that

“While it is never possible to know in advance the losses a bank will suffer in a particular year, a bank can forecast the average level of credit losses it can reasonably expect to experience. These losses are referred to as Expected Losses (EL) ….”

One of the functions of bank capital is to provide a buffer to protect a bank’s debt holders against peak losses that exceed expected levels… Losses above expected levels are usually referred to as Unexpected Losses (UL) – institutions know they will occur now and then, but they cannot know in advance their timing or severity….”

“An Explanatory Note on the Basel II IRB Risk Weight Functions” BCBS July 2005

There was a time when the Internal Ratings Based approach, combining some elegant theory and relatively simple math, seemed to have all the answers

  • A simple intuitive division between expected and unexpected loss
  • Allowing expected loss to be quantified and directly covered by risk margins in pricing while the required return on unexpected loss could be assigned to the cost of equity
  • A precise relationship between expected and unexpected loss, defined by the statistical parameters of the assumed loss distribution
  • The capacity to “control” the risk of unexpected loss by applying seemingly unquestionably strong confidence levels (i.e. typically 1:1000 years plus) to the measurement of target capital requirements
  • It even seemed to offer a means of neatly calibrating the capital requirement to the probability of default of your target debt rating (e.g. a AA senior debt rating with a 5bp probability of default = a 99.95% confidence level; QED)

If only it was that simple … but expected loss is still a good place to start

In practice, the inherently cyclical nature of banking means that the line between expected and unexpected loss is not always as simple or clear as represented above. It would be tempting to believe that the transition to expected loan loss accounting will bring greater transparency to this question but I doubt that is the case. Regulatory Expected Loss (REL) is another possible candidate but again I believe it falls short of what would be desirable for drawing the line that signals where we are increasingly likely to have crossed from the domain of the expected to the unexpected.

The problem (from a capital adequacy perspective) with both IFRS9 and REL is that the “expected” value still depends on the state of the credit cycle at the time we are taking its measure. REL incorporates a Downturn measure of Loss Given Default (DLGD) but the other inputs (Probability of Default and Exposure at Default) are average values taken across a cycle, not the values we expect to experience at the peak of the cycle downturn.

We typically don’t know exactly when the credit cycle will turn down, or by how much and how long, but we can reasonably expect that it will turn down at some time in the future. Notwithstanding the “Great Moderation” thesis that gained currency prior to the GFC, the long run of history suggests that it is dangerous to bet against the probability of a severe downturn occurring once every 15 to 25 years. Incorporating a measure into the Internal Capital Adequacy Process (ICAAP) that captures this aspect of expected loss provides a useful reference point and a potential trigger for reviewing why the capital decline has exceeded expectations.

Uncertainty is by definition not measurable

One of the problems with advanced model based approaches like IRB is that banks experience large value losses much more frequently than the models suggest they should. As a consequence, the seemingly high margins of safety implied by 1:1000 year plus confidence levels in the modelling do not appear to live up to their promise.

A better way of dealing with uncertainty

One of the core principles underpinning this proposal is that the boundary between risk (which can be measured with reasonable accuracy) and uncertainty (which can not be measured with any degree of precision) probably lies around the 1:25 year confidence level (what we usually label a “severe recession). I recognise that reasonable people might adopt a more conservative stance arguing that the zone of validity of credit risk models caps out at 1:15 or 1:20 confidence levels but I am reasonably confident that 1:25 defines the upper boundary of where credit risk models tend to find their limits. Each bank can makes its own call on this aspect of risk calibration.

Inside this zone of validity, credit risk models coupled with stress testing and sensitivity analysis can be applied to generate a reasonably useful estimate of expected losses and capital impacts. There is of course no guarantee that the impacts will not exceed the estimate, that is why we have capital. The estimate does however define the rough limits of what we can claim to “know” about our risk profile.

The “expected versus unexpected” distinction is all a bit abstract – why does it matter?

Downturn loss is part of the risk reward equation of banking and manageable, especially if the cost of expected downturn losses has already been built into credit risk spreads. Managing the risk is easier however if a bank’s risk appetite statement has a clear sense of:

  • exactly what kind of expected downturn loss is consistent with the specific types of credit risk exposure the risk appetite otherwise allows (i.e. not just the current exposure but also any higher level of exposure that is consistent with credit risk appetite) and
  • the impact this would be expected to have on capital adequacy.

This type of analysis is done under the general heading of stress testing for both credit risk and capital adequacy but I have not often seen evidence that banks are translating the analysis and insight into a specific buffer assigned the task of absorbing expected downturn losses and the associated negative impact on capital adequacy. The Cyclical Buffer I have outlined in this post offers a means of more closely integrating the credit risk management framework and the Internal Capital Adequacy Assessment Process (ICAAP).

What gets you into trouble …

“It ain’t what you don’t know that gets you into trouble. It’s what you know for sure that just ain’t so”

Commonly, possibly mistakenly, attributed to Mark Twain

This saying captures an important truth about the financial system. Some degree of volatility is part and parcel of the system but one of the key ingredients in a financial crisis or panic is when participants in the system are suddenly forced to change their view of what is safe and what is not.

This is one of the reasons why I believe that a more transparent framework for tracking the transition from expected to truly unexpected outcomes can add to the resilience of the financial system. Capital declines that have been pre-positioned in the eyes of key stakeholders as part and parcel of the bank risk reward equation are less likely to be a cause for concern or trigger for panic.

The equity and debt markets will still revise their valuations in response but the debt markets will have less reason to question the fundamental soundness of the bank if the capital decline lies within the pre-positioned operating parameters defined by the target cyclical buffer. This will be especially so to the extent that the Capital Conservation Buffer provides substantial layers of additional buffer to absorb the uncertainty and buy time to respond to it.

Calibrating the size of the Cyclical Buffer

Incorporating a Cyclical Buffer does not necessarily mean that a bank needs to hold more capital. It is likely to be sufficient to simply partition a set amount of capital that bank management believes will absorb the expected impact of a cyclical downturn. The remaining buffer capital over minimum requirements exists to absorb the uncertainty and ensure that confidence sensitive liabilities are well insulated from the impacts of that uncertainty.

But first we have to define what we mean by “THE CYCLE”. This is a term frequently employed in the discussion of bank capital requirements but open to a wide range of interpretation.

A useful start to calibrating the size of this cyclical buffer is to distinguish:

  • An economic or business cycle; which seems to be associated with moderate severity, short duration downturns occurring once every 7 to 10 years, and
  • The “financial cycle” (to use a term suggested by Claudio Borio) where we expect to observe downturns of greater severity and duration but lower frequency (say once every 25 years or more).

Every bank makes its own decision on risk appetite but, given these two choices, mine would calibrated to, and hence resilient against, the less frequent but more severe and longer duration downturns associated with the financial cycle.

There is of course another layer of severity associated with a financial crisis. This poses an interesting challenge because it begs the question whether a financial crisis is the result of some extreme external shock or due to failures of risk management that allowed an endogenous build up of risk in the banking system. This kind of loss is I believe the domain of the Capital Conservation Buffer (CCB).

There is no question that banks must be resilient in the face of a financial crisis but my view is that this is a not something that should be considered an expected cost of banking.

Incorporating a cyclical buffer into the capital structure for an Australian D-SIB

Figure 2 below sets out an example of how this might work for an Australian D-SIB that has adopted APRA’s 10.5% CET1 “Unquestionably Strong”: benchmark as the basis of its target capital structure. These banks have a substantial layer of CET1 capital that is nominally surplus to the formal prudential requirements but in practice is not if the bank is to be considered “unquestionably strong” as defined by APRA. The capacity to weather a cyclical downturn might be implicit in the “Unquestionably Strong” benchmark but it is not transparent. In particular, it is not obvious how much CET1 can decline under a cyclical downturn while a bank is still deemed to be “Unquestionably Strong”.

Figure 2 – Incorporating a cyclical buffer into the target capital structure

The proposed Cyclical Buffer sits on top of the Capital Conservation Buffer and would be calibrated to absorb the increase in losses, and associated drawdowns on capital, expected to be experienced in the event of severe economic downturn. Exactly how severe is to some extent a question of risk appetite, unless of course regulators mandate a capital target that delivers a higher level of soundness than the bank would have chosen of its own volition.

In the example laid out in Figure 2, I have drawn the limit of risk appetite at the threshold of the Capital Conservation Buffer. This would be an 8% CET1 ratio for an Australian D-SIB but there is no fundamental reason for drawing the lone on risk appetite at this threshold. Each bank has the choice of tolerating some level of incursion into the CCB (hence the dotted line extension of risk appetite). What matters is to have a clear line beyond which higher losses and lower capital ratios indicate that something truly unexpected is driving the outcomes being observed.

What about the prudential Counter-Cyclical Capital Buffer?

I have deliberately avoided using the term”counter” cyclical in this proposal to distinguish this bank controlled Cyclical Buffer (CyB) from its prudential counterpart, the “Counter Cyclical Buffer” (CCyB), introduced under Basel III. My proposal is similar in concept to the variations on the CCyB being developed by the Bank of England and the Canadian OFSI. The RBNZ is also considering something similar in its review of “What counts as capital?” where it has proposed that the CCyB should have a positive value (indicatively set at 1.5%) at all times except following a financial crisis (see para 105 -112 of the Review Paper for more detail).

My proposal is also differentiated from its prudential counter part by the way in which the calibration of the size of the bank Cyclical Buffer offers a way for credit risk appetite to be more formally integrated with the Internal Capital Adequacy Process (ICAAP) that sets the overall target capital structure.

Summing up

  • Incorporating a Cyclical Buffer into the target capital structure offers a means of more closely integrating the risk exposure and capital adequacy elements of a bank’s risk appetite
  • A breach of the Cyclical Buffer creates a natural trigger point for reviewing whether the unexpected outcomes was due to an unexpectedly large external shock or was the result of credit exposure being riskier than expected or some combination of the two
  • The role of the Capital Conservation Buffer in absorbing the uncertainty associated with risk appetite settings is much clearer if management of cyclical expected loss is assigned to the Cyclical Buffer

What am I missing …

Tony

The Bankers’ New Clothes: Arguments for simpler capital and much reduced leverage

It always pays to make sure you expose yourself to the opposite view. This post looks at some of the arguments for simpler and higher bank capital requirements put forward by Professors Admati and Hellwig. They have published a number of papers and a book on the topic but this post refers chiefly to their book “The Bankers’ New Clothes” and to a paper ‘The Parade of the Banker’s New Clothes Continues: 31 Flawed Claims Debunked”. As I understand it, the key elements of their argument are that:

  • Banks are inherently risky businesses,
  • Excessive borrowing by banks increases their inherent riskiness, but
  • Banks are only able to maintain this excessive level of borrowing because
    • Flawed risk based capital models underestimate the true capital requirements of the business
    • Market discipline also allows excessive borrowing because it is assumed that the government will bail out banks if the situation turns out badly

They identify a variety of ways of dealing with the problem of excessive leverage (controls on bank lending, liquidity requirements and capital requirements) but argue that substantially more common equity is the best solution because:

  • It directly reduces the probability that a bank will fail (i.e. all other things being equal, more common equity reduces the risk of insolvency),
  • A higher level of solvency protection has the added benefit of also reducing the risk of illiquidity, and
  • Contrary to claims by the banking industry, there is no net cost to society in holding more common equity because the dilution in ROE will be offset by a decline in the required return on equity

They concede that there will be some cost associated with unwinding the Too Big To Fail (TBTF) benefit that large banks currently enjoy on both the amount banks can borrow and on the cost of that funding but argue there is still no net cost to society in unwinding this undeserved subsidy. The book, in particular, gets glowing reviews for offering a compelling case for requiring banks to operate with much lower levels of leverage and for pointing out the folly of risk based capital requirements.

There are a number of areas where I find myself in agreement with the points they argue but I can’t make the leap to accept their conclusion that much a higher capital requirement based on a simple leverage ratio calculation is the best solution. I have written this post to help me think through the challenges they offer my beliefs about how banks should be capitalised.

It is useful, I think, to first set out the areas where we (well me at least) might agree in principle with what they say; i.e.

  • Financial crises clearly do impose significant costs on society and excessive borrowing does tend to make a financial system fragile (the trick is to agree what is “excessive”)
  • Better regulation and supervision have a role to play in minimising the risk of bank failure (i.e. market discipline alone is probably not enough)
  • Public policy should consider all costs, not just those of the banking industry
  • All balance sheets embody a trade-off between enterprise risk, return and leverage (i.e. increasing leverage does increase risk)

It is less clear however that:

  • The economics of bank financing are subject to exactly the same rules as that which apply to non-financial companies (i.e. rather than asserting that banks should be compared with non-financial companies, it is important to understand how banks are different)
  • A policy of zero failure for banks is necessarily the right one, or indeed even achievable (i.e. would it be better to engineer ways in which banks can fail without dragging the economy down with them)
  • Fail safe mechanisms, such as the bail in of pre-positioned liabilities, have no prospect of working as intended
  • The assertion that “most” of the new regulation intended to make banks safer and easier to resolve has been “rejected, diluted or delayed” is a valid assessment of what has actually happened under Basel III
  • That liquidity events requiring lender of last resort support from the central bank are always a solvency problem

Drawing on some previous posts dealing with these issues (see here, here and here), I propose to focus on the following questions:

  • How does the cost of bank financing respond to changes in leverage?
  • Are the risk based capital requirements as fundamentally flawed as the authors claim?
  • Are risk management incentives for bankers always better when they are required to hold increasing levels of common equity?
  • Do the increased loss absorption features of Basel III compliant hybrids (in particular, the power to trigger conversion or bail in of the instruments) offer a way to impose losses on failed banks without disrupting the economy or requiring public support

How does leverage affect the cost of bank financing?

Increasing the proportion of equity funding, the authors argue, reduces the risk that shareholders are exposed to because each dollar of equity they have invested

“ will be affected less intensely by the uncertainty associated with the investments”

“when shareholders bear less risk per dollar invested, the rate of return they require is lower”

“Therefore, taking the costs of equity as fixed and independent of the mix of equity and debt involves a fundamental fallacy”.

Banker’sNew Clothes (p101)

The basic facts they set out are not really contentious; the mix of debt and equity does impact required returns. The authors focus on what happens to common equity but changing leverage impacts both debt and equity. This is very clear in the way that rating agencies consider all of the points nominated by the authors when assigning a debt rating. Reduced equity funding will likely lead to a decline in the senior and subordinated debt ratings and higher costs (plus reduced access to funding in absolute dollar terms) while higher equity will be a positive rating factor.

Banks are not immune to these fundamental laws but it is still useful to understand how the outcomes are shaped by the special features of a bank balance sheet. My views here incorporate two of the claims they “debunk” in their paper; specifically

Flawed Claim #4: The key insights from corporate finance about the economics of funding, including those of Modigliani and Miller, are not relevant for banks because banks are different from other companies

Flawed Claim #5: Banks are special because they create money

One of the features that defines a bank is the ability to take deposits. The cost of deposits however tends to be insulated from the effects of leverage. This is a design feature. Bank deposits are a major component of the money supply but need to be insensitive to adverse information about the issuing bank to function as money.

Wanting bank deposits to be information insensitive does not make them so. That is a function of their super senior position in the liability loss hierarchy, supplemented in many, if not most, banking systems by some form of limited deposit insurance (1). I credit a paper by Gary Gorton and George Pennacchi titled “Financial Intermediaries and Liquidity Creation” for crytalising this insight (an earlier post offers a short summary of that paper). Another paper titled “Why Bail-In? And How?” by Joseph Sommer proposes a different rationale for deposits having a super senior position insulated from the risk of insolvency but the implications for the impact of leverage on bank financing costs are much the same.

A large bank also relies on senior unsecured financing. This class of funding is more risky than deposits but still typically investment grade. This again is a design feature. Large banks target an investment grade rating in order to deliver, not only competitive financing costs, but equally (and perhaps more importantly) access to a larger pool of potential funding over a wider range of tenors. The investment grade rating depends of course on there being sufficient loss absorbing capital underwriting that outcome. There is no escaping this law of corporate finance. 

The debt rating of large banks is of course also tied up with the issue of banks being treated as Too Big To Fail (TBTF). That is a distortion in the market that needs to be addressed and the answer broadly is more capital though the rating agencies are reasonably agnostic on the form this capital should take in so far as the senior debt rating is concerned. Subject to having enough common equity anchoring the capital structure, more Tier 2 subordinated debt (or Tier 3 bail-in) will work just as well as more common equity for the purposes of reducing the value of implied government support currently embedded in the long term senior debt rating.

Admati and Hellwig are right – there is no free lunch in corporate finance

At this stage, all of this risk has to go somewhere. On that point I completely agree with Admati and Hellwig. There is no free lunch, the rating/risk of the senior tranches of financing depend on having enough of the right kinds of loss absorbing capital standing before them in the loss hierarchy. Where I part company is on the questions of how much capital is enough and what form it should take.

How much capital is (more than) enough?

Admati and Hellwig’s argument for more bank capital has two legs. Firstly, they note that banks are typically much more leveraged than industrial companies and question how can this be given the fundamental law of capital irrelevancy defined by Modigliani and Miller. Secondly, they argue that risk based capital requirements are fundamentally flawed and systematically under estimate how much capital is required.

Why are banks different?

Admati and Hellwig note that banks have less capital than industrial companies and conclude that this must be a result of the market relying on the assumption that banks will be bailed out. The existence of a government support uplift in the senior debt ratings of large banks is I think beyond debate. There is also broad support (even amongst many bankers) that this is not sound public policy and should ideally be unwound.

It is not obvious however that this wholly explains the difference in observed leverage. Rating agency models are relatively transparent in this regard (S&P in particular) and the additional capital required to achieve a rating uplift equivalent to the existing government support factor would still see banks more leveraged than the typical industrial company. Bank balance sheets do seem to be different from those of industrial companies.

Flawed risk models

The other leg to their argument is that risk based capital fundamentally under estimates capital requirements. I am broadly sympathetic to the sceptical view on how to use the outputs of risk models and have been for some time. An article I wrote in 2008, for example, challenged the convention of using a probability of default associated with the target debt rating to precisely calibrate the amount of capital a bank required.

The same basic concept of highly precise, high confidence level capital requirements is embedded in the Internal Ratings Based formula and was part of the reason the model results were misinterpreted and misused. Too many people assigned a degree of precision to the models that was not warranted. That does not mean however that risk models are totally useless.

Professors Admati and Hellwig use simple examples (e.g. how does the risk of loss increase if a personal borrower increases leverage on a home loan) to argue that banks need to hold more capital. While the basic principle is correct (all other things equal, leverage does increase risk), the authors’ discussion does not draw much (or possibly any?) attention to the way that requiring a borrower to have equity to support their borrowing reduces a bank’s exposure to movements in the value of the loan collateral.

In the examples presented, any decline in the value of the assets being financed flows through directly to the value of equity, with the inference that this would be true of a bank also. In practice, low risk weights assigned by banks to certain (low default – well secured) pools of lending reflect the existence of borrower’s equity that will absorb the first loss before the value of the loan itself is called into question.

A capital requirement for residential mortgages (typically one of the lowest risk weights and also most significant asset classes) that looks way too low when you note that house prices can easily decline by 10 or 20%, starts to make more sense when you recognise that that there is (or should be) a substantial pool of borrower equity taking the brunt of the initial decline in the value of collateral. The diversity of borrowers is also an important factor in reducing the credit risk of the exposures (though not necessarily the systemic risk of an overall meltdown in the economy). Where that is not the case (and hence the renewed focus on credit origination standards and macro prudential policy in general), then low risk weights are not justified.

I recognise that this argument (incorporating the value of the borrower’s equity) does not work for traded assets where the mark to market change in the value of the asset flows directly to the bank’s equity. It does however work for the kinds of assets on bank balance sheets that typically have very low risk weights (i.e. the primary concern of the leverage ratio advocates). It also does not preclude erring on the side of caution when calculating risk weights so long as the model respects the relative riskiness of the various assets impacting the value of equity.

How much also depends on the quality of risk management (and supervision)

The discussion of how much capital a bank requires should also recognise the distinction between how much a well managed bank needs and how much a poorly managed bank needs. In a sense, the authors are proposing that all banks, good and bad, should be made to hold the capital required by bad banks. Their focus on highlighting the risks of banking obscures the fact that prudent banking mitigates the downside and that well managed banks are not necessarily consigned to the extremes of risk the authors present as the norm of banking.

While not expressed in exactly that way, the distinction I am drawing is implicit in Basel III’s Total Loss Absorbing Capital (TLAC) requirements now being put in place. TLAC adds a substantial layer of additional loss absorption on top of already substantially strengthened common equity requirements. The base layer of capital can be thought of as what is required for a well managed, well supervised bank with a sound balance sheet and business model. APRA’s “Unquestionably Strong” benchmark for CET1 is a practical example of what this requirement looks like. The problem of course is that all banks argue they are good banks but the risk remains that they are in fact bad banks and we usually don’t find out the difference until it is too late. The higher TLAC requirement provides for this contingency.

What should count as capital?

I looked at this question in a recent post on the RBNZ’s proposal that virtually all of their TLAC requirement should be comprised of common equity. Admati and Hellwig side with the RBNZ but I believe that a mix of common equity and bail-in capital (along the lines proposed by APRA) is the better solution.

Read my earlier post for the long version, but the essence of my argument is that bail-in capital introduces a better discipline over bank management risk appetite than does holding more common equity. Calibrating common equity requirements to very high standards should always be the foundation of a bank capital structure. Capital buffers in particular should be calibrated to withstand very severe external shocks and to be resilient against some slippage in risk management.

The argument that shareholders’ need to have more “skin in the game” is very valid where the company is undercapitalised. Bail-in capital is not a substitute for getting the basics right. A bank that holds too little common equity, calibrated to an idealised view of both its own capabilities and of the capacity of the external environment to surprise the modellers, will likely find itself suppressing information that does not fit the model. Loss aversion then kicks in and management start taking more risk to win back that which was lost, just as Admati and Hellwig argue.

However, once you have achieved a position that is unquestionably strong, holding more common equity does not necessarily enhance risk management discipline. My experience in banking is that it may in fact be more likely to breed an undesirable sense of complacency or even to create pressure to improve returns. I know that the later is not a a winning strategy in the long run but in the short run the market frequently does not care.

What is the minimum return an equity investor requires?

One of the problems I find with a simplistic application of Modigliani & Miller’s (M&M) capital irrelevancy argument is that it does not seem to consider if there is a minimum threshold return for an equity investment below which the investment is no longer sufficiently attractive to investors who are being asked to take first loss positions in a company; i.e. where is the line between debt and equity where a return is simply not high enough to be attractive to equity investors?

Reframing the question in this way suggests that the debate between the authors and the bankers may be more about whether risk based capital adequacy models (including stress testing) can be trusted than it is about the limitations of M&M in the real world.

Summary

The author’s solution to prudential supervision of banks is a shock and awe approach to capital that seeks to make the risk of insolvency de minimus for good banks and bad. I have done my best to be open to their arguments and indeed do agree with a number of them. My primary concern with the path they advocate is that I do not believe the extra “skin in the game” generates the risk management benefits they claim.

I see more potential in pursuing a capital structure based on

  • a level of common equity that is robustly calibrated to the needs of a well managed (and well supervised) bank
  • incorporating a well designed counter cyclical capital buffer,
  • supplemented with another robust layer of bail-in capital that imposes real costs (and accountability) on the shareholders and management of banks for whom this level of common equity proves insufficent.

The authors argue that the authorities would never use these bail-in powers for fear of further destabilising funding markets. This is a valid area of debate but I believe they conflate the risks of imposing losses on bank depositors with the kinds of risks that professional bond investors have traditionally absorbed over many centuries of banking. The golden era in which the TBTF factor shielded bank bondholders from this risk is coming to the end but this broader investment class of bond holders has dealt with defaults by all kinds of borrowers. I am not sure why banks would be special in this regard if countries can default. The key issue is that the investors enter into the contract with the knowledge that they are at risk and are being paid a risk premium commensurate with the downside (which may not be that large if investors judge the banks to be well managed).

This is a complex topic so please let me know if I have missed something fundamental or have otherwise mis-represented Admati and Hellwig’s thesis. In the interim, I remain mostly unconvinced …

Tony

  1. It is worth noting that NZ has adopted a different path with respect to deposit protection, rejecting both deposit preference and deposit insurance. They also have a unique policy tool (Open Bank Resolution) that allows the RBNZ to impose losses on deposits as part of the resolution process. They are reviewing the case for deposit insurance and I believe should also reconsider deposit preference.

How much capital is enough? – The NZ perspective

The RBNZ has delivered the 4th instalment in a Capital Review process that was initiated in March 2017 and has a way to run yet. The latest consultation paper addresses the question “How much capital is enough?”.  The banking industry has until 29 March 2019 to respond with their views but the RBNZ proposed answer is:

  • A Tier 1 capital requirement of 16% of RWA for systemically important banks and 15% of RWA for all other banks
  • The Tier 1 minimum requirement to remain unchanged at 6% (with AT1 capital continuing to be eligible to contribute a maximum of 1.5 percentage points)
  • The proposed increased capital requirement to be implemented via an overall prudential capital buffer of 9-10% of RWA comprised entirely of CET1 capital;
    • Capital Conservation Buffer 7.5% (currently 2.5%)
    • D-SIB Buffer 1.0% (no change)
    • Counter-cyclical buffer 1.5% (currently 0%)

The increase in the capital ratio requirement is proposed to be supplemented with a series of initiatives that will increase the RWA of IRB banks:

  • The RBNZ proposes to 1) remove the option to apply IRB RW to sovereign and bank exposures,  2) increase the IRB scalar (from 1.06 to 1.20) and 3) to introduce an output floor set at 85% of the Standardised RWA on an aggregate portfolio basis
  • As at March 2018, RWA’s produced by the IRB approach averaged 76% of the Standardised Approach and the RBNZ estimate that the overall impact will be to increase the aggregate RWA to 90% of the outcome generated by the Standardised approach (i.e. the IRB changes, not the output floor, drive the increase in RWA)
  • Aggregate RWA across the four IRB banks therefore increases by approximately 16%, or $39bn, compared to March 2018 but the exact impact will depend on how IRB banks respond to the higher capital requirements

The RBNZ has also posed the question whether a Tier 2 capital requirement continues to be relevant given the substantial increase in Tier 1 capital.

Some preliminary thoughts …

There is a lot to unpack in this paper so this post will only scratch the surface of the issues it raises …

  • The overall number that the RBNZ proposes (16%) is not surprising.It looks to be at the lower end of what other prudential regulators are proposing in nominal terms
  • But is in the same ball park once you allow for the substantial increase in IRB RWA and the fact that it is pretty much entirely CET1 capital
  • What is really interesting is the fundamentally different approach that the RBNZ has adopted to Tier 2 capital and bail-in versus what APRA (and arguably the rest of the world) has adopted
    • The RBNZ proposal that the increased capital requirement take the form of CET1 capital reflects its belief that “contingent convertible instruments” should be excluded from what counts as capital
    • Exactly why the RBNZ has adopted this position is a complex post in itself (their paper on the topic can be found here) but the short version (as I understand it) is that they think bail-in capital instruments triggered by non-viability are too complex and probably won’t work anyway.
    • Their suggestion that Tier 2 probably does not have a role in the capital structure they have proposed is logical if you accept their premise that Point of Non-Viability (PONV) triggers and bail-in do not work.
  • The RBNZ highlight a significantly enhanced role for prudential capital buffersI am generally in favour of bigger, more dynamic, capital buffers rather than higher fixed minimum requirements and I have argued previously in favour of the base rate for the counter-cyclical being a positive value (the RBNZ propose 1.5%)
    • But the overall size of the total CET1 capital buffer requirement requires some more considered thought about 1) the role of bail-in  structures and PONV triggers in the capital regulation toolkit (as noted above) and 2) whether the impacts of the higher common equity requirement will be as benign as the RBNZ analysis suggests
  • I am also not sure that the indicative capital conservation responses they have outlined (i.e. discretionary distributions limited to 60% of net earnings in the first 250bp of the buffer, falling to 30% in the next 250bp and no distributions thereafter) make sense in practice.
    • This is because I doubt there will be any net earnings to distribute if losses are sufficient to reduce CET1 capital by 250bp so the increasing capital conservation requirement is irrelevant.
  • Last, but possibly most importantly, we need to consider the impact on the Australian parents of the NZ D-SIB banks and how APRA responds. The increase in CET1 capital proposed for the NZ subsidiaries implies that, for any given amount of CET1 capital held by the Level 2 Banking Group, the increased strength of the NZ subsidiaries will be achieved at the expense of the Australian banking entities
    • Note however that the impact of the higher capital requirement in NZ will tend to be masked by the technicalities of how bank capital ratios are calculated.
      • It probably won’t impact the Level 2 capital ratios at all since these are a consolidated view of the combined banking group operations of the Group as a whole
      • The Level 1 capital ratios for the Australian banks also treat investments in bank subsidiaries relatively generously (capital invested in unlisted subsidiaries is treated as a 400% risk weighted asset rather than a capital deduction).

Conclusion

Overall, I believe that the RBNZ is well within its rights to expect the banks it supervises to maintain a total level of loss absorbing capital of 16% or more. The enhanced role for capital buffers is also a welcome move.

The issue is whether relying almost entirely on CET1 capital is the right way to achieve this objective. This is however an issue that has been debated for many decades with no clear resolution. It will take some time to fully unpack the RBNZ argument and figure out how best to articulate why I disagree. In the interim, any feedback on the issues I have outlined above would be most welcome.

Tony

Loss absorption under bail-in

I recently did a post on a Discussion Paper setting out how APRA proposes to increase the Loss Absorption Capital (LAC) of Australian authorised deposit-taking institutions (ADIs). I came down on the side of this being a desirable (arguably necessary) enhancement of the Australian financial system but noted that the devil was in the detail. One of the issues discussed was the potential impact of the proposal on the statutory and contractual loss hierarchy that defines the sequence in which losses are absorbed by the capital of the bank in the first instance, and by more senior sources of funding in need.  

This post attempts to dig a bit deeper into this question to better understand how losses would be assigned under a bail-in scenario. It is a pretty technical point and possibly of limited interest but I wanted to make sure I had a good handle on how loss absorption plays out in the future. Read on or stop here.

Key points

  • The bail-in of selected, pre-positioned liabilities modifies the traditional loss hierarchy that applies in a liquidation scenario 
    • As a general rule, the absorption of losses is accelerated across all tiers of LAC
    • CET1 investors bear the loss via the dilution of their shareholdings as AT1 and Tier 2 are converted to common equity
    • AT1 investors risk not receiving distributions but otherwise the loss hierarchy between them and T2 investors seems to collapse once their holdings are converted into CET1
    • The only potential advantage to Tier 2 in these scenarios is that these instruments may only face partial conversion but how beneficial depends on the extent to which conversion to common equity offers a better chance to liquidate their holding versus selling the Tier 2 instrument itself into what is likely to be a very illiquid market
  • This has been increasingly true since APRA introduced Point of Non-Viability (PONV) conversion triggers in 2013, and the instruments without this contractual feature progressively matured, but the proposed expansion of the pool of LAC takes us further down this path:
    • partly by virtue of making it easier for APRA to restructure bank capital structures without recourse to taxpayer support (i.e. the odds of bail-in being used in a future crisis are increased if the tool itself is more effective); and
    • partly by increasing the quantum of CET1 dilution that is the mechanism by which losses are allocated to the various tiers of LAC
  • Investors in the various capital tiers will obviously adjust the return they require for the risks they are asked to bear but we should ensure we all have a clear and consistent understanding of how the loss hierarchy is modified, and whether the resulting loss hierarchy is desirable (or indeed equitable)
  • The answer to this question turns in part on whether the outcomes for AT1 and T2 investors are better or worse than the market value they could achieve if they sold their investments prior to bail-in 

Loss Hierarchy – the simple version

Prudential Standard APS 111 (Capital Adequacy: Measurement of Capital) defines the order of seniority amongst the three tiers of prudential capital:

  • CET1 Capital “… rank behind the claims of depositors and other more senior creditors in the event of a winding up of the issuer ” (Para 19 (d))
  • AT1 Capital “… rank behind the claims of depositors and other more senior creditors in the event of a winding up of the issuer” (Para 28 (c))
  • Tier 2 Capital “represents, prior to any conversion to Common Equity Tier 1 … the most subordinated claim in liquidation of the issuer after Common Equity Tier 1 Capital instruments and Additional Tier 1 Capital instruments (Attachment H, Para 1 (b))

APS 111 (Attachment F, Para 10) also explicitly allows AT1 instruments to 1) differentiate as to whether the instrument is required to convert or be written-off in the first instance, and 2) provide for a ranking under which individual AT1 instruments will be converted or written-off. The guidance on Tier 2 is less explicit on this point but there does not seem to be any fundamental reason why a bank could not introduce a similar ranking within the overall level of subordination. I am not aware of any issuer using this feature for either AT1 or T2.

If we ignore for a moment the impact of bail-in (either by conversion or write-off), the order in which losses are applied to the various sources of funding employed by a company follows this loss hierarchy:

  • Going Concern:
    • Common Equity Tier 1 (CET1)
    • Additional Tier 1 (AT1)
  • Insolvency – Liquidation or restructuring:
    • Tier 2 (T2)
    • Senior unsecured
    • Super senior
      • Covered bonds
      • Deposits
      • Insured deposits

CET1 is clearly on the front line of loss absorption (a perpetual commitment of funding with any returns subject to the issuer having profits to distribute and the Capital Conservation Ratio (CCR) not being a constraint). AT1 is subject to similar restrictions, though its relative seniority does offer some protection regarding the payment of regular distributions.

Traditionally, the claims the other forms of funding have on the issuer are only at risk in the event of the liquidation or restructuring of the company but bail-in modifies this traditional loss hierarchy.

What happens to the loss hierarchy under bail in?

First up, let’s define bail-in …

“A bail-in is the rescue of a financial institution that is on the brink of failure whereby creditors and depositors take a loss on their holdings. A bail-in is the opposite of a bailout, which involves the rescue of a financial institution by external parties, typically governments that use taxpayers money.” (Investopedia)

Investopedia’s definition above is useful, albeit somewhat generic. Never say never, but the loss hierarchy employed in Australia, combined with the fact that there are substantial layers of more junior creditors for big banks in particular, means that most Australian depositors (even the ones that do not have the benefit of deposit insurance) are pretty well insulated from bail-in risk. Not everyone would share my sanguine view on this question (i.e. the limited extent to which deposits might be bailed in) and some countries (NZ for example) quite explicitly choose to forego deposit insurance and move deposits up the loss hierarchy by ranking them equally with senior unsecured creditors.

The main point of bail-in is that existing funding is used to recapitalise the bank, as opposed to relying on an injection of new capital from outside which may or may not be forthcoming. It follows that pre-positioning sufficient layers of loss absorption, and making sure that investors understand what they have signed up for, is critical.

AT1 has always been exposed to the risk of its distributions being cut. This sounds good in theory for loss absorption but the size of these potential capital outflows is relatively immaterial in any real stress scenario. It could be argued that every dollar helps but my view is that the complexity and uncertainty introduced by making these distributions subject to the Capital Conservation Ratio (CCR) outweigh any contribution they might make to recapitalising the bank. The people who best understand this point are those who have had to calculate the CCR in a stress scenario (you have to get into the detail to understand it). The CCR issue could be addressed by simplifying the way it is calculated and I would argue that simplicity is always a desirable feature of any calculation that has to be employed under conditions of stress and uncertainty. The main point however is that it does very little to help recapitalise the bank because the heavy lifting in any really severe stress scenario depends on the capacity to convert a pool of pre-positioned, contingent capital into CET1.

APRA has had explicit power to bail-in AT1 and T2 since the January 2013 version of APS 111 introduced Point of Non-Viability (PONV) conversion triggers – these enhanced powers do a few things:

  • The impact of losses is brought forward relative what would apply in a conventional liquidation or restructuring process
  • For CET1 investors, this accelerated impact is delivered via the dilution of their shareholdings (and associated share price losses)
  • In theory, conversion shields the AT1 investors from loss absorption because they receive common equity equivalent in value to the book value of their claim on the issuer
  • In practice, it is less clear that the AT1 investors will be able to sell the shares at the conversion price or better, especially if market liquidity is adversely impacted by the events that called the viability of the issuer into question
  • The conversion challenge will be even greater to the extent that T2 investors are also bailed-in and seek to sell the shares they receive

Tier 2 will only be bailed-in after AT1 bail-in has been exhausted, as would be expected given its seniority in the loss hierarchy, but it is hard to see a bail-in scenario playing out where the conversion of AT1 alone is sufficient to restore the viability of the bank. AT1 is likely to represent not much more than the 1.5 percentage points of RWA required to meet minimum requirements but any crisis sufficient to threaten the viability of a bank is likely to require a much larger recapitalisation so full or partial conversion of T2 should be expected.

Partial conversion 

Attachment J – Para 6 provides that “Conversion or write-off need only occur to the extent necessary to enable APRA to conclude that the ADI is viable without further conversion or write-off”. Para 8 of the same attachment also specifies that “An ADI may provide for Additional Tier 1 Capital instruments to be converted or written off prior to any conversion or write-off of Tier 2 Capital instruments”.

This makes it reasonably clear that APRA will not automatically require all AT1 and Tier 2 to be converted or written-off but the basis on which partial conversion would be applied is not covered in the discussion paper. A pro-rata approach (i.e. work out how much of the aggregate Tier 2 is required to be converted and then apply this ratio to each  individual instrument) seems the simplest option and least open to legal challenge but it may be worth considering alternatives.

Converting the Tier 2 instruments closest to maturity in particular seems to offer some advantages over the pro rata approach

  • It generates more CET1 capital than the Tier 2 foregone (because the Tier 2 capital value of an instrument is amortised in its final 5 years to maturity whereas the CET1 capital created by bail-in is the full face value off the instrument)
  • It defers the need to replace maturing Tier 2 capital and maximises the residual pool of LAC post bail-in.

What is the reason for the 20% floor that APS 111 imposes on the conversion price?

The transition to a bail-in regime may be an opportune time to revisit the rationale for placing a floor on the conversion price used to convert AT1 and Tier 2 into common equity. Attachments E and F contain an identically worded paragraph 8 that requires that the share price used to calculate the shares received on conversion cannot be less than 20% of the ordinary share price at the the time the LAC instrument was issued. This floor arguably requires the share price to fall a long way before it has any effect but it is not clear what purpose is served by placing any limit on the extent to which common equity shareholders might see their holdings diluted in a non-viability scenario.

Bail-in via write-off of AT1 or T2

I am concentrating on bail-in via conversion because that seems to be the default loss absorption contemplated by APS 111 and the one that is most consistent with the traditional loss hierarchy. LAC instruments can be designed with write-off as the primary loss absorption mechanism but it is not clear that any issuer would ever choose to go down that path as it would likely be more expensive versus bail-in via conversion. The write-off option seems to have been included as a failsafe in the event that conversion is not possible for whatever reason.

Conclusion

The loss absorption hierarchy under a bail-in based capital regime is a bit more complicated than the simple, progressive three tier hierarchy that would apply in a traditional liquidation scenario. I believe however that this added complexity is justified both by the enhanced level of financial safety and by the extent to which it addresses the advantage big banks have previously enjoyed by virtue of being Too Big To Fail.

The main concern is that AT1 and Tier 2 investors who underwrite the pre-positioning of this contingent source of new CET1 capital properly understand the risks. I must confess that I had to think it through and remain open to the possibility that I have missed something … if so tell me what I am missing.

Tony

 

Does more loss absorption and “orderly resolution” eliminate the TBTF subsidy?

The Australian Government’s 2014 Financial System Inquiry (FSI) recommended that APRA implement a framework for minimum loss-absorbing and recapitalisation capacity in line with emerging international practice, sufficient to facilitate the orderly resolution of Australian authorised deposit-taking institutions (ADIs) and minimise taxpayer support (Recommendation 3).

In early November, APRA released a discussion paper titled “Increasing the loss absorption capacity of ADIs to support orderly resolution” setting out its response to this recommendation. The paper proposes that selected Australian banks be required to hold more loss absorbing capital. Domestic Systemically Important Banks (DSIBs) are the primary target but, depending partially on how their Recovery and Resolution Planning addresses the concerns APRA has flagged, some other banks will be captured as well.

The primary objectives are to improve financial safety and stability but APRA’s assessment is that competition would also be “Marginally improved” on the basis that “requiring larger ADIs to maintain additional loss absorbency may help mitigate potential funding advantages that flow to larger ADIs“. This assessment may be shaped by the relatively modest impact (5bp) on aggregate funding costs that APRA has estimated or simple regulatory conservatism. I suspect however that APRA is under selling the extent to which the TBTF advantage would be mitigated if not completely eliminated by the added layer of loss absorption proposed. If I am correct, then this proposal would in fact, not only minimise the risk to taxpayers of future banking crises, but also represent an important step forward in placing Australian ADIs on a more level playing field.

Why does the banking system need more loss absorption capacity?

APRA offers two reasons:

  1. The critical role financial institutions play in the economy means that they cannot be allowed to fail in a disorderly manner that would have adverse systemic consequences for the economy as a whole.
  2. The government should not be placed in a position where it believes it has no option but to bail out one or more banks

The need for extra capital might seem counter-intuitive, given that ADI’s are already “unquestionably strong”, but being unquestionably strong is not just about capital, the unstated assumption is that the balance sheet and business model are also sound. The examples that APRA has used to calibrate the degree of total loss absorption capacity could be argued to reflect scenarios in which failures of management and/or regulation have resulted in losses much higher than would be expected in a well-managed banking system dealing with the normal ups and downs of the business cycle.

At the risk of over simplifying, we might think of the first layers of the capital stack (primarily CET1 capital but also Additional Tier 1) being calibrated to the needs of a “good bank” (i.e. well-managed, well-regulated) while the more senior components (Tier 2 capital) represent a reserve to absorb the risk that the good bank turns out to be a “bad bank”.

What form will this extra capital take?

APRA concludes that ADI’s should be required to hold “private resources” to cope with this contingency. I doubt that conclusion would be contentious but the issue is the form this self-insurance should take. APRA proposes that the additional loss absorption requirement be implemented via an increase in the minimum Prudential Capital Requirement (PCR) applied to the Total Capital Ratio (TCR) that Authorised Deposit-Taking Institutions (ADIs) are required to maintain under Para 23 of APS 110.

“The minimum PCRs that an ADI must maintain at all times are:
(a) a Common Equity Tier 1 Capital ratio of 4.5 per cent;
(b) a Tier 1 Capital ratio of 6.0 per cent; and
(c) a Total Capital ratio of 8.0 per cent.
APRA may determine higher PCRs for an ADI and may change an ADI’s PCRs at any time.”

APS 110 Paragraph 23

This means that banks have discretion over what form of capital they use, but APRA expect that banks will use Tier 2 capital that counts towards the Total Capital Ratio as the lowest cost way to meet the requirement. Advocates of the capital structure irrelevance thesis would likely take issue with this part of the proposal. I believe APRA is making the right call (broadly speaking) in supporting more Tier 2 rather than more CET1 capital, but the pros and cons of this debate are a whole post in themselves. The views of both sides are also pretty entrenched so I doubt I will contribute much to that 50 year old debate in this post.

How much extra loss absorbing capital is required?

APRA looked at three things when calibrating the size of the additional capital requirement

  • Losses experienced in past failures of systemically important banks
  • What formal requirements other jurisdictions have applied to their banks
  • The levels of total loss absorption observed being held in an international peer group (i.e. what banks choose to hold independent of prudential minimums)

Based on these inputs, APRA concluded that requiring DSIBs to maintain additional loss absorbing capital of between 4-5 percentage points of RWA would be an appropriate baseline setting to support orderly resolution outcomes. The calibration will be finalised following the conclusion of the consultation on the discussion paper but this baseline requirement looks sufficient to me based on what I learned from being involved in stress testing (for a large Australian bank).

Is more loss absorption a good idea?

The short answer, I think, is yes. The government needs a robust way to recapitalise banks which does not involve risk to the taxpayer and the only real alternative is to require banks to hold more common equity.

The devil, however, is in the detail. There are a number of practical hurdles to consider in making it operational and these really need to be figured out (to the best of out ability) before the fact rather than being made up on the fly under crisis conditions.  The proposal also indirectly raises some conceptual issues with capital structure that are worth understanding.

How would it work in practice?

The discussion paper sets out “A hypothetical outcome from resolution action” to explain how an orderly resolution could play out.

“The approximate capital levels the D-SIBs would be expected to maintain following an increase to Total Capital requirements, and a potential outcome following the use of the additional loss absorbency in resolution, are presented in Figure 6. Ultimately, the outcome would depend on the extent of losses.

If the stress event involved losses consistent with the largest of the FSB study (see Figure 2), AT1 and Tier 2 capital instruments would be converted to ordinary shares or written off. After losses have been considered, the remaining capital position would be wholly comprised of CET1 capital. This conversion mechanism is designed to allow for the ADI to be stabilised in resolution and provide scope to continue to operate, and particularly to continue to provide critical functions.”

IMG_5866.JPG

Source – APRA Discussion Paper (page 24)

What I have set out below draws from APRA’s example while adding detail that hopefully adds some clarity on what should be expected if these scenarios ever play out.

  • In a stress event, losses first impact any surplus CET1 held in excess of the Capital Conservation Buffer (CCB) requirement, and then the CCB itself (the first two layers of loss absorption in Figure 6 above)
  • As the CCB is used up, the ADI is subject to progressive constraints on discretionary distributions on CET1 and AT1 capital instruments
  • In the normal course of events, the CCB should be sufficient to cope with most stresses and the buffer is progressively rebuilt through profit retention and through new issuance, if the ADI wants to accelerate the pace of the recapitalisation process
  • The Unquestionably Strong capital established to date is designed to be sufficient to allow ADIs to withstand quite severe expected cyclical losses (as evidenced by the kinds of severe recession stress scenarios typically used to calibrate capital buffers)
  • In more extreme scenarios, however, the CCB is overwhelmed by the scale of losses and APRA starts to think about whether the ADI has reached a Point of Non-Viability (PONV) where ADI’s find themselves unable to fund themselves or to raise new equity; this is where the proposals in the Discussion Paper come into play
  • The discussion paper does not consider why such extreme events might occur but I have suggested above that one reason is that the scale of losses reflects endogenous weakness in the ADI (i.e. failures of risk management, financial control, business strategy) which compound the losses that would be a normal consequence of downturns in the business cycle
  • APRA requires that AT1 capital instruments, classified as liabilities under Australian Accounting Standards, must include a provision for conversion into ordinary shares or write off when the CET1 capital ratio falls to, or below 5.125 per cent
  • In addition, AT1 and Tier 2 capital instruments must contain a provision, triggered on the occurrence of a non-viability trigger event, to immediately convert to ordinary shares or be written off
  • APRA’s simple example show both AT1 and Tier 2 being converted to CET1 (or write-off) such that the Post Resolution capital structure is composed entirely of CET1 capital

Note that conversion of the AT1 and Tier 2 instruments does not in itself allocate losses to these instruments. The holders receive common equity equivalent to the book value of their instrument which they can sell or hold. The ordinary shareholders effectively bear the loss via the forced dilution of their shareholdings. The main risk to the ATI and Tier 2 holders is that, when they sell the ordinary shares received on conversion, they may not get the same price that which was used to convert their instrument. APRA also imposes a floor on the share price that is used for conversion which may mean that the value of ordinary shares received is less than the face value of the instrument being converted. The reason why ordinary shareholders should be protected in this way under a resolution scenario is not clear.

The devil is in the detail – A short (probably incomplete) list of issues I see with the proposal:

  1. Market capacity to supply the required quantum of additional Tier 2 capital required
  2. Conversion versus write-off
  3. The impact of conversion on the “loss hierarchy”
  4. Why not just issue more common equity?
  5. To what extent would the public sector continue to stand behind the banking system once the proposed level of self insurance is in place?

Market capacity to supply the required level of additional loss absorption

APRA has requested industry feedback on whether market appetite for Tier 2 capital will be a problem but its preliminary assessment is that:

” … individual ADIs and the industry will have the capacity to implement the changes necessary to comply with the proposals without resulting in unnecessary cost for ADIs or the broader financial system.

Preliminary estimates suggest the total funding cost impact from increasing the D-SIBs’Total Capital requirements would not be greater than five basis points in aggregate based on current spreads. Assuming the D-SIBs meet the increased requirement by increasing the issuance of Tier 2 capital instruments and reducing the issuance of senior unsecured debt, the impact is estimated by observing the relative pricing of the different instruments. The spread difference between senior unsecured debt and Tier 2 capital instruments issued by D- SIBs is around 90 to 140 basis points.”

I have no expert insights on this question beyond a gut feel that the required level of Tier 2 capital cannot be raised without impacting the current spread between Tier 2 capital and senior debt, if at all. The best (only?) commentary I have seen to date is by Chris Joye writing in the AFR (see here and here). The key points I took from his opinion pieces are:

  • The extra capital requirement translates to $60-$80 billion of extra bonds over the next four years (on top of rolling over existing maturities)
  • There is no way the major banks can achieve this volume
  • Issuing a new class of higher ranking (Tier 3) bonds is one option, though APRA also retains the option of scaling back the additional Tier 2 requirement and relying on its existing ability to bail-in senior debt

Chris Joye know a lot more about the debt markets than I do, but I don’t think relying on the ability to bail-in senior debt really works. The Discussion Paper refers to APRA’s intention that the “… proposed approach is … designed with the distinctive features of the Australian financial system in mind, recognising the role of the banking system in channelling foreign savings into the economy “ (Page 4). I may be reading too much into the tea leaves, but this could be interpreted as a reference to the desirability of designing a loss absorbing solution which does not adversely impact the senior debt rating that helps anchor the ability of the large banks to borrow foreign savings. My rationale is that the senior debt rating impacts, not only the cost of borrowing, but also the volume of money that foreign savers are willing to entrust with the Australian banking system and APRA specifically cites this factor as shaping their thinking. Although not explicitly stated, it seems to me that APRA is trying to engineer a solution in which the D-SIBs retain the capacity to raise senior funding with a “double A” rating.

Equally importantly, the creation of a new class of Tier 3 instruments seems like a very workable alternative to senior bail-in that would allow the increased loss absorption target to be achieved without impacting the senior debt rating. This will be a key issue to monitor when ADI’s lodge their response to the discussion paper. It also seems likely that the incremental cost of the proposal on overall ADI borrowing costs will be higher than the 5bp that APRA included in the discussion paper. That is not a problem in itself to the extent this reflects the true cost of self insurance against the risk of failure, just something to note when considering the proposal.

Conversion versus write-off

APRA has the power to effect increased loss absorption in two ways. One is to convert the more senior elements of the capital stack into common equity but APRA also has the power to write these instruments off. Writing off AT1 and/or T2 capital, effectively represents a transfer of value from the holders of these instruments to ordinary shareholders. That is hard to reconcile with the traditional loss hierarchy that sees common equity take all first losses, with each of the more senior tranches progressively stepping up as the capacity of more junior tranches is exhausted.

Consequently I assume that the default option would always favour conversion over write-off. The only place that I can find any guidance on this question is Attachment J to APS 111 (Capital Adequacy) which states

Para 11. “Where, following a trigger event, conversion of a capital instrument:

(a)  is not capable of being undertaken;

(b)  is not irrevocable; or

(c) will not result in an immediate and unequivocal increase in Common Equity Tier 1 Capital of the ADI,

the amount of the instrument must immediately and irrevocably be written off in the accounts of the ADI and result in an unequivocal addition to Common Equity Tier 1 Capital.”

That seems to offer AT1 and Tier 2 holders comfort that they won’t be asked to take losses ahead of common shareholders but the drafting of the prudential standard could be clearer if there are other reasons why APRA believe a write-off might be the better resolution strategy. The holders need to understand the risks they are underwriting but ambiguity and uncertainty are to helpful when the banking system is in, or a risk of, a crisis.

The impact of conversion on the “loss hierarchy”

The concept of a loss hierarchy describes the sequence under which losses are first absorbed by common equity and then by Additional Tier 1 and Tier 2 capital, if the more junior elements prove insufficient. Understanding the loss hierarchy is I think fundamental to understanding capital structure in general and this proposal in particular:

  • In a traditional liquidation process, the more senior elements should only absorb loss when the junior components of the capital stack are exhausted
  • In practice, post Basel III, the more senior elements will be required to participate in recapitalising the bank even though there is still some book equity and the ADI technically solvent (though not necessarily liquid)
  • This is partly because the distributions on AT1 instruments are subject to progressively higher capital conservation restrictions as the CCB shrinks but mostly because of the potential for conversion to common equity (I will ignore the write-off option to keep things simple)

I recognise that APRA probably tried to simplify this explanation but the graphic example they used (see Figure 6 above) to explain the process shows the Capital Surplus and the CCB (both CET1 capital) sitting on top of the capital stack followed by Tier 2, Additional Tier 1 and finally the minimum CET1 capital. The figure below sets out what I think is a more logical illustration of the capital stack and loss .

IMG_2739

Losses initially impact CET1 directly by reducing net tangible assets per share. At the point of a non-viability based conversion event, the losses impact ordinary shareholders via the dilution of their shareholding. AT1 and Tier 2 holders only share in these losses to the extent that they sell the ordinary shares they receive for less than the conversion price (or if the conversion price floor results in them receiving less than the book value of their holding).

Why not just issue more common equity?

Capital irrelevancy M&M purists will no doubt roll their eyes and say surely APRA knows that the overall cost of equity is not impacted by capital structure tricks. The theory being that any saving in the cost of using lower cost instruments, will be offset by increases in the costs (or required return) of more subordinated capital instruments (including equity).

So this school argues you should just hold more CET1 and the cost of the more senior instruments will decline. The practical problem I think is that, the cost of senior debt already reflects the value of the implied support of being too big, or otherwise systemically important, to be allowed to fail. The risk that deposits might be exposed to loss is even more remote partly due to deposit insurance but, possibly more importantly, because they are deeply insulated from risk by the substantial layers of equity and junior ranking liabilities that must be exhausted before assets are insufficient to cover deposit liabilities.

To what extent would the public sector continue to stand behind the banking system once the proposed level of self insurance is in place?

Assuming the market capacity constraint question could be addressed (which I think it can), the solution that APRA has proposed seems to me to give the official family much greater options for dealing with future banking crises without having to call on the taxpayer to underwrite the risk of recapitalising failed or otherwise non-viable banks.

It does not, however, eliminate the need for liquidity support. I know some people argue that this is a distinction without a difference but I disagree. The reality is that banking systems built on mostly illiquid assets will likely face future crises of confidence where the support of the central bank will be necessary to keep the financial wheels of the economy turning.

There are alternative ways to construct a banking system. Mervyn King, for example, has advocated a version of the Chicago Plan under which all bank deposits must be 100% backed by liquid reserves that would be limited to safe assets such as government securities or reserves held with the central bank. Until we decide to go down that path, or something similar, the current system requires the central bank to be the lender of last resort. That support is extremely valuable and is another design feature that sets banks apart from other companies. It is not the same however, as bailing out a bank via a recapitalisation.

Conclusion

I have been sitting on this post for a few weeks while trying to consider the pros and cons. As always, the risk remains that I am missing something. That said, this looks to me like a necessary (and I would argue desirable) enhancement to the Australian financial system that not only underpins its safety and stability but also takes us much closer to a level playing field. Big banks will always have the advantage of sophistication, scale and efficiency that comes with size but any funding cost advantage associated with being too big to fail now looks to be priced into the cost of the additional layers of loss absorption this proposal would require them to put in place.

Tony